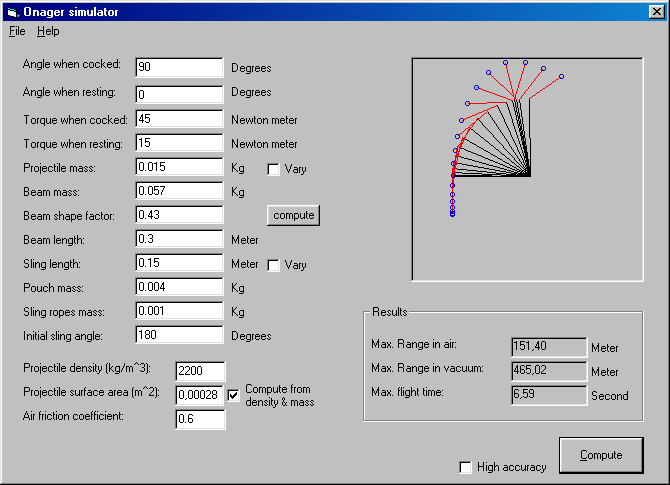
The onager simulator

The onager simulator calculates all aspects of a roman onager, such as the projectile acceleration during launch and almost 20 other physical parameters that you may need to design an onager. Range is computed with air resistance.

The program allows you to vary certain parameters, like sling length and mass to draw a graph of sling length versus range.

The program is freeware, including the full visual basic source code. Download here (1.8 Mb, version 1.0.1). Feel free to alter the source code.

Output

The result window allows you to plot any physical parameter of the simulation against each other. If you do a calculation with fixed sling length/mass, the most useful plots are those with time on the horizontal axis, and some other parameter on the vertical. The little white sphere indicates the optimal release time.

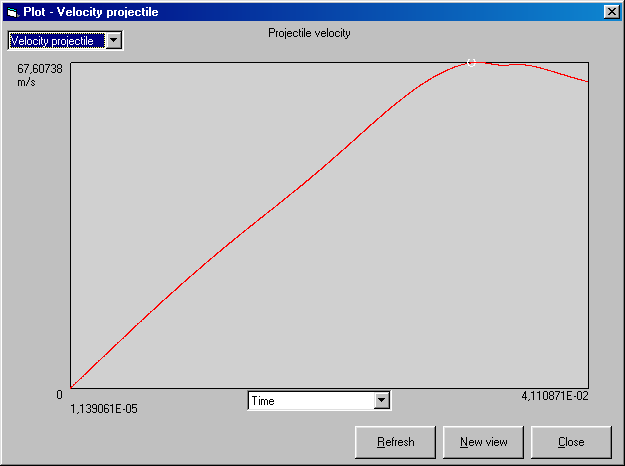
If you do a calculation where the sling length is varied, make sure that you choose 'sling length' on the horizontal axis. In this case the 'time' parameter will be the time of release. The other parameters will also be the values they had at the time of projectile release and may not be of much value.

Some parameters are only available if you vary the sling length or mass. These are:
sling length, range in air, projectile mass, range efficiency in vacuum, range efficiency in air and maximal lateral force

Comparison to real world onagers

I think the simulation gives ranges that are larger than real-world onagers. (My own onager throws about 70% of the computed range) I think there are two reasons for this:

- There may be additional friction in the skein ropes. So if it takes 100 Newton meter of torque to put down the beam, you may get only 50 Newton Meter effective when you release it. However I am not at all sure about this.

- The air friction coefficient may be very difficult to determen, especially for small irregular projectiles.

If the simulator gives ranges that are too high, you should try reducing the torque and keep in mind this is only a simulation; The real world is notoriously difficult to simulate.

Other notes:

- Beam shape factor=0.58 for uniform beam, 0.4 for a properly tapered one. Definition:
{shape factor}={beam inertia moment}/({beam mass}*{beam length}2)

- Simulation may be slightly inaccurate when beam stalls.

- The peak in acceleration may be incredibly high when the beam stalls. This is caused by centrifugal forces.

- enter the torque corrected for friction in the skein.

- torque=length * force = length * 9.8 * (weight to put it down)

- Air friction coefficient may be higher than 1.0 for irregular objects

- Acceleration is in m/s2. Divide by 9.8 to get G-force.

- To get an bitmap of the graphs: press alt-printscreen in the windows, then open paint and select edit-->paste in the menu.

- All measures are expressed in SI units.

- The calculation of the maximal range in air takes relatively a lot of time. Therefore, this is computed only at the estimated time of release. This time of release is determend by searching for the maximum range in vacuum. Obviously this is not entirely correct but it saves a lot of computing/programming effort.

- Density table:
water/vegatables1000 kg/m3
rock2200
iron7900
gold19300

- Skein mass is ignored

- Gravity is ignored until after release

Known bugs in version 1.0.0: (now solved)

- The time indicated in the graph showes twice the actual time.

Links:

This document
       The original of this document.
My onager
       My small onager
The Algorithmic Beauty of the Trebuchet
       Has a trebuchet calculator
Easy Job Timer
       One of my shareware programs. Easy job timer is a timing application that allows you to track the time you spend on tasks for clients or other activities. The application is intended to be very easy to use.
MDG Software
       My personal homepage

program created by 2000

(c) , , 25 Dec 2000